Photomacrography Theory Back to Notes on Photography
by Makoto Honda December 4, 2005 Topcon RE Super/ Topcon Super D Photos Topcon Bellows Setup Photos
General
In photomacrography, the large lens extension needed when focusing on a close-up subject results in an exposure factor (X) that cannot be ignored.
Just very simplistically stated, when the lens is focused at infinity, the lens-film distance is the focal length of the lens. If it is a 50mm lens, the lens is placed at the distance 50mm away from the film. In terms of this lens extension, the magnification, M, is defined as:
M = L (mm) / F (mm)
where F is the focal length of the lens, and L is the lens extension beyond the infinity setting (i.e., L = 0 when the lens is set at infinity). For instance, if you extend the lens by the same distance as the focal length, then M = F / F, and you are shooting a photograph at magnification 1.
Of course, the more general description of the magnification is the size of the image on the film relative to the actual size of the subject being photographed:
M = Image size / Subject size
If a subject having a width of W mm is filling the horizontal extent (36mm) of the 35 mm picture frame, the magnification is given by:
M = 36 (mm) / W (mm)
The exposure factor, X, for this magnification is calculated as:
X = square of (M + 1)
The f-stop increase (I) for this exposure factor is:
2 to the power of I = X
or
I = log 2 X
Table 1 shows the exposure factor for various magnifications for both the 35mm format (36 x 24mm) and the APS-C format (24 x 16mm) photography.
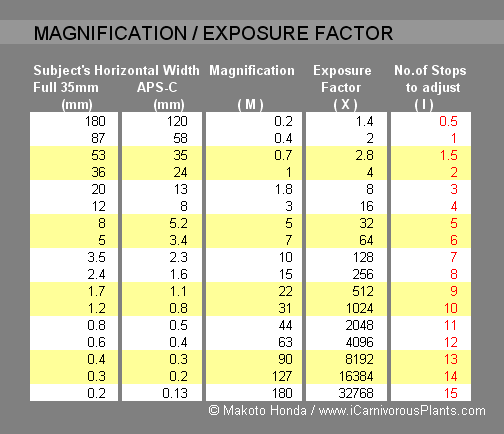
Table 1
How to Use the Tables
The purpose of this table is to determine the amount of the exposure increase needed for a given magnification. Find the actual dimension of the subject depicted along the horizontal width of your viewfinder. (Use the appropriate format: Full 35mm or APS-C format.) Following the row found in the table for your subject width, find the number of F-stops (rightmost column) needed to be compensated for the corresponding exposure factor for this magnification.
Let's suppose your magnification is M = 1.8. This means you are enlarging a 20mm subject to cover the entire 36mm width of the full 35mm frame; you get the same magnification for a 13mm wide subject for the APS-C format. Table 1 shows the number of stops for this magnification to be 3. What this means is this. Let's say you are setting the lens aperture at F16 for this shooting. The F16 is the marking on the lens you are using. To obtain the "effective" f-number, you must go 3 stops from the lens aperture the lens is set at.
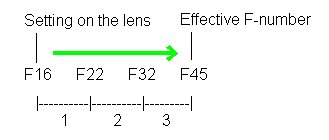
Because of the
greater lens extension needed to get this high magnification, the real f-number
("effective" f-number) is F45. You must calculate the exposure based on this F45
aperture, not F16, even if you are using the F16 setting on the lens.
If you are relying on the camera's TTL (Through-The-Lens) exposure meter, this "darkening" effect of the lens is automatically taken into consideration by the meter. If you are using an external flash for illumination, however, the flash distance must be calculated based on the effective aperture of the setup, not the aperture marked on the lens.
Photomacrography is notorious for two reasons. One is an extreme requirement for lighting, exactly because of the exposure factor we described above. The other is the loss of definition of the image coming from the diffraction of light. Note that the maximum theoretical resolution limit is based on the effective f-number calculated above. In a high magnification photography, you may find a sharp decline in the image resolution, say, from F11 to F16. It is because after considering the proper exposure factor of the setup, your actual effective f-numbers might be F32 and F45!
Discussion
Let's look at the table. For example, if the subject measuring 72mm wide is occupying the entire horizontal frame of the 35mm format viewfinder, the magnification becomes:
M = 36mm / 72mm = 0.5
Note that the table does not show all numbers in fine increment, so you may have to extrapolate. If the subject measuring 36mm wide is magnified to cover the entire horizontal frame, the magnification is exactly 1.0 as below:
M = 36mm / 36mm = 1.0
If the same subject measuring 36mm wide is magnified to the entire horizontal frame of the APS-C format (24mm wide) camera, the magnification would become:
M = 24mm / 36mm = 2 / 3 = 0.67
This means, to take the same photograph with the small er APS-C format, compared with the full-35mm format, requires less magnification. This is just a factual observation of the film format as it relates to the magnification. This, in and of itself, does not imply that it is better or worse to use the small er format camera because you can get the same photograph with a lesser magnification.
Perspective Consideration
In high magnification photomacrography, say, the magnification above M = 2, the consideration of the image "perspective" becomes pretty much meaningless, because of the extremely shallow depth of field obtainable in such magnification. So just choose the lens (focal length) most convenient to work with that gives you the desired magnification. (See Perspective Retention in Photomacrography.)
Easy Reference
I created this table for myself as an easy reference for photomacrography. The table tells me which lens+bellows combination gives the magnification I want. Find the actual subject width that fills the horizontal extent of the frame, and I know which lens I should use on my bellows to get that magnification. (Use the appropriate column depending on the format: Full 35mm or APS-C format.) The table also gives me the number of stops to adjust for the exposure compensation.
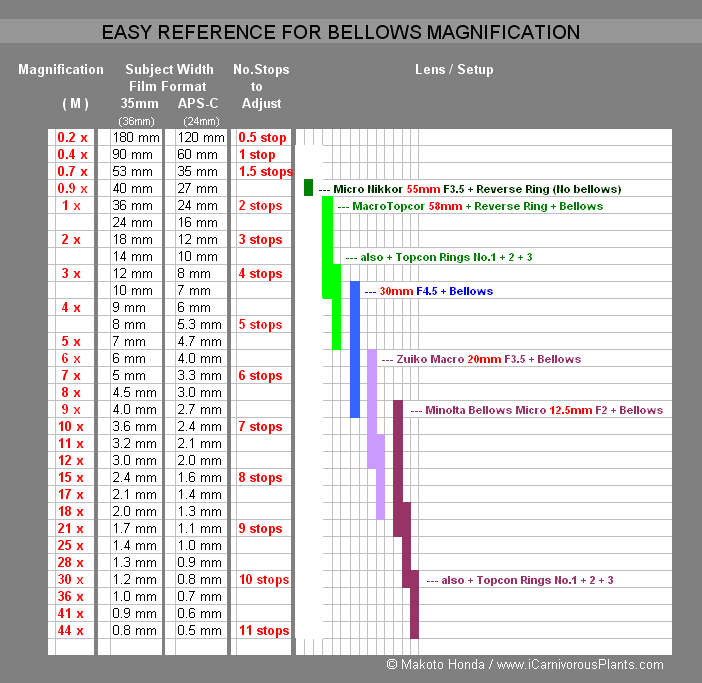
Table 2
Looking at the table, we see that, for any given setup, the magnification is the same for both the 35mm and the APS-C formats. For instance, a camera setup where a 36mm wide subject is filling the 36mm width of the 35mm format yields the magnification of 1. Without changing the setup at all, just replace the camera with the one having the APS-C format. The magnification (M = 1) remains the same:. Now, since this is a small er format, however, 24mm wide portion of the subject is filling the 24mm width of the APS-C format.
Note carefully that this does not produce the same photograph. If you are to make the same 8x10 print from each of the formats, the image from the APS-C format shows a more enlarged view of the subject, because the image, in effect, has been cropped due to the small er format size.
| Carnivorous Plants Photography Web Site: Copyright © 2001-2018 Makoto Honda. All Rights Reserved. |